Cooperation among mobile individuals with payoff expectations in the spatial prisoner’s dilemma game

Abstract

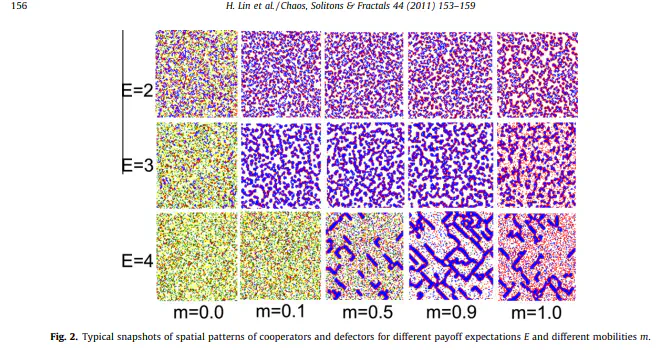
We propose a model to address the problem how the evolution of cooperation in a social system depends on the spatial motion and the payoff expectation. In the model, if the actual payoff of an individual is smaller than its payoff expectation, the individual will either move to a new site or simply reverse its current strategy. It turns out that migration of dissatisfied individuals with relatively low expectation level leads to the aggregation of cooperators and promotion of cooperation. Moreover, under appropriate parameters migration leads to some interesting spatiotemporal patterns which seems not to have been reported in previously studied spatial games. Furthermore, it also found that a population with constant expectation can better favor cooperative behavior than a population with adaptive aspiration.