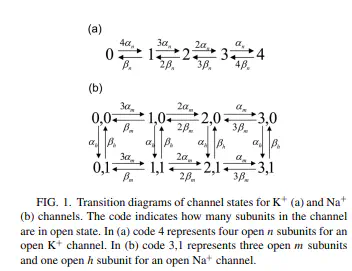
Abstract
Stochasticity in ion channel gating is the major source of intrinsic neuronal noise, which can induce many important effects in neuronal dynamics. Several numerical implementations of the Langevin approach have been proposed to approximate the Markovian dynamics of the Hodgkin-Huxley neuronal model. In this work an improved channel-based Langevin approach is proposed by introducing a truncation procedure to limit the state fractions in the range of [0, 1]. The truncated fractions are put back into the state fractions in the next time step for channel noise calculation. Our simulations show that the bounded Langevin approaches combined with the restored process give better approximations to the statistics of action potentials with the Markovian method. As a result, in our approach the channel state fractions are disturbed by two terms of noise an uncorrelated Gaussian noise and a time-correlated noise obtained from the truncated fractions. We suggest that the restoration of truncated fractions is a critical process for a bounded Langevin method.