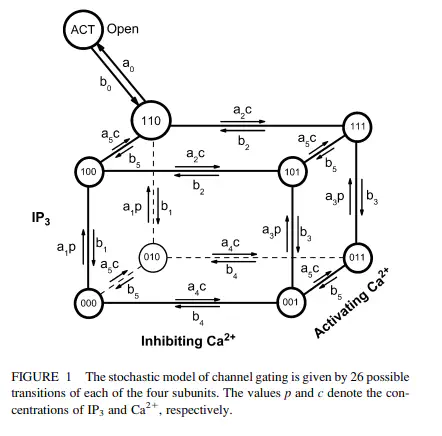
Abstract
Intracellular calcium release is a prime example for the role of stochastic effects in cellular systems. Recent models consist of deterministic reaction-diffusion equations coupled to stochastic transitions of calcium channels. The resulting dynamics is of multiple time and spatial scales, which complicates far-reaching computer simulations. In this article, we introduce a novel hybrid scheme that is especially tailored to accurately trace events with essential stochastic variations, while deterministic concentration variables are efficiently and accurately traced at the same time. We use finite elements to efficiently resolve the extreme spatial gradients of concentration variables close to a channel. We describe the algorithmic approach and we demonstrate its efficiency compared to conventional methods. Our single-channel model matches experimental data and results in intriguing dynamics if calcium is used as charge carrier. Random openings of the channel accumulate in bursts of calcium blips that may be central for the understanding of cellular calcium dynamics.