Abstract
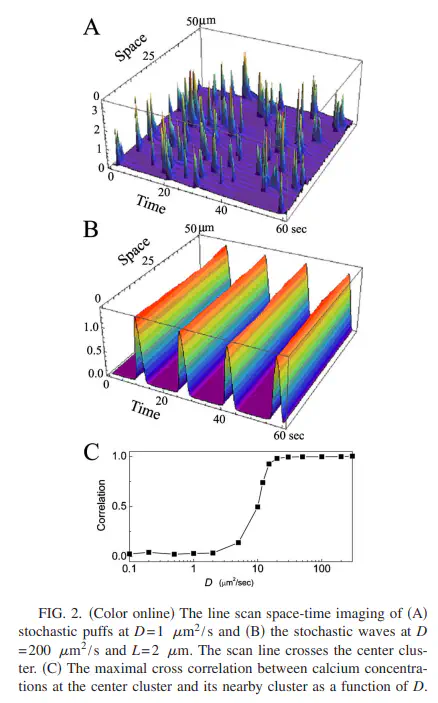
In many cell types, calcium ion channels on the endoplasmic reticulum membrane occur in a clustered distribution. The channels generate either localized puffs, each comprising channels of only one cluster, or global calcium waves. In this work we model the calcium system as a two-dimensional lattice of active elements distributed regularly in an otherwise passive space. We address an important feature of the puff-wave transition, which is the difference in lifetime of puffs at a few hundred milliseconds and long-lived global waves with periods of several seconds. We show that such a lifetime difference between puffs and waves can be understood with strongly reduced ordinary differential equations modified by a time-scale factor that takes into account the coupling strength of active and passive regions determined by the Ca2+ diffusion coefficient. Furthermore, we show that the point model can also describe very well the dependence of Ca2+ oscillation characteristics on the cluster-cluster distance in the case of large diffusivity.