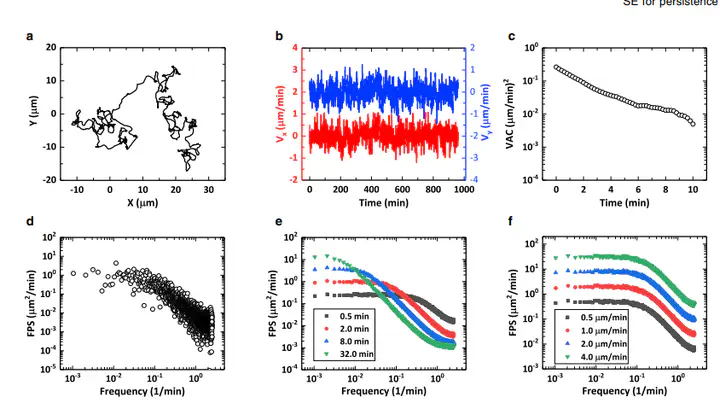
Abstract
Cell migration, which can be significantly affected by intracellular signaling pathways and extracellular matrix,plays a crucial role in many physiological and pathological processes. Cell migration is typically modeled as a persistent random walk, which depends on two critical motility parameters, i.e., migration speed and persistence time. It is generally very challenging to efficiently and accurately quantify the migration dynamics from noisy experimental data. Here, we introduce the normalized Shannon entropy (SE) based on the FPS of cellular velocity autocovariance function to quantify migration dynamics.The SE introduced here possesses a similar physical interpretation as the Gibbs entropy for thermal systems in that SE naturally reflects the degree of order or randomness of cellular migration, attaining the maximal value of unity for purely diffusive migration (i.e., SE ¼ 1 for the most ‘‘random’’ dynamics) and the minimal value of 0 for purely ballistic dynamics (i.e., SE ¼ 0 for the most ‘‘ordered’’ dynamics). We also find that SE is strongly correlated with the migration persistence but is less sensitive to the migrattion speed. Moreover, we introduce the time-varying SE based on the WPS of cellular dynamics and demonstrate its superior utility to characterize the time-dependent persistence of cell migration, which typically results from complex and time-varying intra- or extracellular mechanisms. We employ our approach to analyze experimental data of in vitro cell migration regulated by distinct intracellular and extracellular mechanisms, exhibiting a rich spectrum of dynamic characteristics. Our analysis indicates that the SE and wavelet transform (i.e., SE-based approach) offers a simple and efficient tool to quantify cell migration dynamics in complex microenvironment.